Cơ Học Lưu Chất
BÀI TẬP CHƯƠNG I
MỞ ĐẦU
Bài 1.1
Để làm thí nghiệm thủy lực, người ta đổ đầy nước vào một đường ống có đường kính d = 300mm, chiều dài L = 50m
ở áp suất khí quyển. Hỏi lượng nước cần thiết phải đổ vào ống là bao nhiêu để áp suất đạt tới 51at ? Biết hệ số nén
ép β p =
1
at −1
20000
Giải
Lượng nước cần thiết phải đổ vào ống để áp suất tăng lên 51at là :
Ta có hệ số giãn nở do áp lực : β p = −
Do dV , dp đồng biến nên : β p = +
Mà thể tích
⇒ dV =
V = S .L =
1 dV
⇒ dV = β p .V .dp
V dp
1 dV
⇒ dV = β p .V .dp
V dp
π .d 2
3,14.(0.3) 2
.L =
.50 = 3,5325m 3
4
4
1
.3,5325.(51 − 1) = 8,84.10 −3 (m 3 ) = 8,84 (liter )
20000
Vậy cần phải thêm vào ống 8.84 lít nước nữa để áp suất tăng từ 1at lên 51at.
Bài 1.2
Trong một bể chứa hình trụ thẳng đứng có đường kính d = 4m, đựng 100 tấn dầu hỏa có khối lượng riêng
ρ = 850kg / m 3 ở 100C. Xác định khoảng cách dâng lên của dầu trong bể chứa khi nhiệt độ tăng lên đến 40 0C. Bỏ
0
qua giãn nở của bể chứa. Hệ số giãn nở vì nhiệt β t = 0,00072 C
−1
.
Giải
Khối lượng riêng của dầu hỏa là : ρ =
m
m 100.10 3 2000
⇒V = =
=
≈ 117,65(m 3 )
V
ρ
850
17
Hệ số giãn nở do nhiệt độ :
βt =
1 dV
2000
216
⇒ dV = β t .V .dt = 0,00072.
.(40 − 30) =
≈ 2,542(m 3 )
V dt
17
85
Mà : dV =
π .d 2
4dV 4.2,542
.∆h ⇒ ∆h =
=
= 0,202(m)
4
π .d 2 3,14.4 2
Vậy khoảng cách dầu dâng lên so với ban đầu là 0.202(m)
Bài 1.3
Khi làm thí nghiệm thủy lực, dùng một đường ống có đường kính d = 400mm, dài L = 200m, đựng đầy nước ở áp
suất 55 at. Sau một giờ áp suất giảm xuống còn 50 at. Xác định lượng nước chảy qua các kẽ hở của đường ống. Hệ
số nén ép β p =
1
at −1 .
20000
Giải
Hệ số giãn nở do áp lực :
Page 1 of 28
Cơ Học Lưu Chất
βp = −
1 dV
π .d
⇒ dV = − β p .V .dp = − β p
.L.dp
V dp
4
⇒ dV = −
2
1 3,14.0,4 2
.200. (50 − 55) = 6,28.10 −3 ( m 3 ) = 6,28 (liter )
20000
4
Vậy lựơng nước chảy qua khe hở đường ống là 6.28 (liter)
Bài 1.4
Một bể hình trụ đựng đầy dầu hỏa ở nhiệt độ 5 0C, mực dầu cao 4m. Xác định mực dầu tăng lên, khi nhiệt độ tăng
lên 250C. Bỏ qua biến dạng của bể chứa. Hệ số giãn nở vì nhiệt β t = 0.00072 C
0
−1
.
Giải
Hệ số giãn nở do nhiệt độ : β t =
1 dV
⇒ dV = β t .V .dt
V dt
π .d 2
.h
4
π .d 2
∆h
Thể tích dầu tăng lên : dV =
4
1 dV
∆h
βt =
=
V dt
h.dt
⇒ ∆h = β t .h.dt = 0,00072.4.(25 − 5) = 0,058(m) = 58(mm)
Mà thể tích ban đầu là : V =
Page 2 of 28
Cơ Học Lưu Chất
BÀI TẬP CHƯƠNG II
THỦY TĨNH HỌC
Bài 2.1
Xác định độ cao của cột nước dâng lên trong ống đo áp (h). Nước trong bình kín chịu áp suất tại
mặt tự do là
p 0t = 1.06at . Xác định áp suất p 0t nếu h = 0.8m.
Giải
Chọn mặt đẳng áp tại mặt thoáng của chất lỏng.
Ta có : p A = p B
p A = p0
⇒ p 0 = p a + γ .h
p B = p0 + γ , h
Mà
⇒h=
p0 − p a (1,06 − 1).9,81.10 4
=
= 0,6 ( m)
γ
9810
Nếu h=0,8m thì ⇒ p0 = γ .h + p a = 9810.0,8 + 98100 = 105948 N / m
2
= 1,08 (at )
Bài 2.2
Một áp kế đo chênh thủy ngân, nối với một bình đựng nước.
a) Xác định độ chênh mực nước thủy ngân, nếu h1 = 130mm và áp suất dư trên mặt nước trong bình 40000 N/
m.
2
b) Áp suất trong bình sẽ thay đổi như thế nào nếu mực thủy ngân trong hai nhánh bằng nhau.
Giải
a) Xác định độ chênh mực thủy ngân (tìm h2) :
Chọn mặt đẳng áp như hình vẽ :
Ta có :
p A = pB
p A = p 0 + γ H 2O .(h1 + h2 )
p B = p a + γ Hg .h2
⇒ p0 + γ H 2O .(h1 + h2 ) = p a + γ Hg .h2
⇔ h2 (γ Hg − γ H 2O ) = ( p 0 − p a ) + γ H 2O .h1
Mà p0 − pa = p d
Vậy : h2 =
p d + γ H 2O .h1
(γ H 2O − γ Hg )
=
40000 + 9810.0,013
= 0,334 (m)
132890 − 98100
Page 3 of 28
b) Áp suất trong bình khi mực thủy ngân trong hai nhánh bằng nhau :
Ta có :
Cơ Học Lưu Chất
pC = p D
pC = p0 + γ H 2O .h
p D = pa
⇒ p0 + γ H 2O .h = p a
⇔ γ H 2O .h = p a − p0 = p ck
⇔ p ck = γ H 2O .h = γ H 2O .(h1 + 1 2 h2 )
1
= 9810.(0,13 + .0,334) = 2913,57 ≈ 0,0297 (at )
2
Bài 2.3
Một áp kế vi sai gồm một ống chữ U đường kính d = 5mm nối hai bình có đường kính D = 50mm với nhau. Máy
đựng đầy hai chất lỏng không trộn lẫn với nhau, có trọng lượng riêng gần bằng nhau : dung dịch rượu êtylic trong
nước ( γ 1 = 8535 N / m 3 ) và dầu hỏa ( γ 2 = 8142 N / m 3 ). Lập quan hệ giữa độ chênh lệch áp suất
∆p = p1 − p2 của khí áp kế phải đo với độ dịch chuyển của mặt phân cách các chất lỏng (h) tính từ vị trí ban đầu
của nó (khi ∆p = 0 ). Xác định ∆p khi h = 250mm.
Giải
a) Lập mối quan hệ giữa độ chênh lệch áp suất ∆p = p1 − p2 :
Chọn mặt đẳng áp như hình vẽ :
•
Khi ∆p = 0 ( p1 = p 2 ) : thì mặt phân cách giữa hai lớp chất lỏng khác nhau ở vị trí cân bằng O :
o
p A = pB
o
p A = p1 + γ 1.h1
o
p B = p2 + γ 2 .h2
Theo điều kiện bình thông nhau : γ 1.h1 = γ 2 h2 ⇒ h1 =
•
γ 2 h2
γ1
Khi ∆p > 0 ( p1 > p2 ) : thì mực nước trong bình 1 hạ xuống 1 đoạn ∆h và đồng thời mực nước bình 2 tăng
lên 1 đoạn ∆h . Khi đó mặt phân cách di chuyển lên trên 1 đoạn h so với vị trí O.
p A = p1 + γ 1.(h1 − ∆h)
p B = p2 + γ 2 .( h2 + ∆h − h) + γ 1.h
Theo tính chất mặt đẳng áp ta có :
p1 + γ 1.( h1 − ∆h) = p2 + γ 2 .(h2 + ∆h − h) + γ 1.h
⇔ p1 − p 2 = γ 2 .(h2 + ∆h − h) − γ 1.(h1 − ∆h) + γ 1.h
⇔ p1 − p 2
...
--------------------------------------
... 23 of 28
Cơ Học Lưu Chất
BÀI TẬP CHƯƠNG V
DÒNG CHẢY QUA LỖ, VÒI
Bài 5.7
Xác định thời gian nước chảy hết một bể chứa lăng trụ, độ sâu nước trong bể H = 4m; có diện tích đáy Ω = 5m 2 ,
qua hai lỗ tròn, lỗ nằm ở thành bên cách đáy e = 2m và một lỗ ở đáy. Kích thước hai lỗ giống nhau d = 10 cm. Cho
hệ số lưu lượng µ = 0.6
Giải
Ta có T = T1 + T2 (bỏ qua v0)
T1 – thời gian qua 2 lỗ (mực nước từ H → He)
T2 – thời gian qua lỗ đáy (khoảng e)
T – thời gian tháo toàn bộ
Lưu lượng lỗ bên : Qb = µ . A1
( h − e) 2 g
Lưu lượng lỗ đáy : Qđ = µ . A2
2 gh
T1 =
H −e
Ω.dh
∫ − µ.ω. 2 g ( h − e + h )
H
=
Ω.
µ .ω.e 2 g
H −e
∫(
H
)
=−
Ω.
H −e
∫
µ .ω. 2 g
H
Ω.
dh
h−e + h
H −e
3
2 3
2
2 − h 2
(
)
h − e + h dh =
h
−
e
3
µ .ω.e 2 g 3
H
2
Ω.
( H − 2e ) 3 2 − 2( H − e ) 3 2 + 4 3 2
=
3 µ .ω.e 2 g
=
2
3
5
( 4 − 2.2 ) 3 2 − 2( 4 − 2 ) 3 2 + 4 3 2 = 187,1 ( s )
π .0,12
2. 2.9,81
4
2.Ω..e
2.5.2
T2 =
=
= 677,5 ( s )
µ .ω. 2 ge
π .0,12
0,6
2.9,81.2
4
T = 187,1 + 677,6 = 864,6 ( s ) = 14′24,6′′
0,6.
Page 24 of 28
Cơ Học Lưu Chất
Bài 5.8
Tính thời gian tháo cạn bể chứa nước hình lăng trụ hình thang dài L = 4m, chiều rộng mặt thoáng B = 5m. Cho hệ
số lưu lượng µ = 0.6 .
Giải
Diện tích của mặt thoáng
Ω = MN.L
Mà MN = b + Ω.MP
MP
h
=
Ta có tỉ lệ : B − b
H
2
B−b
h
2 h
MP =
=
H
5
8
⇒ Ω = 12 + h
5
Thời gian để nước chảy hết bể là :
H2
T =−∫
Ω.dh
H1 M . A.
2 gh
=
1
πd
µ.
4
.65,6 = 52′23′′
2
2 gh
Vậy thời gian để nước chảy hết bể là 52′23′′
Bài 5.9
Tính thời gian tháo hết nước trong bể chứa hình trụ tròn có đường kính d = 2.4m, cao H = 6m trong 2 trường hợp.
a. Bể chứa dựng đứng, ở đáy có khoét lỗ, diện tích ω = 1.76 dm 2
b. Bể chứa nằm ngang, ở đáy có khoét lỗ, cũng có diện tích ω = 1.76 dm 2
Cho biết trong cả hai trường hợp, mặt thoáng của bể đều thống với khí trời.
Giải
1. Bể chứa dựng đứng :
π .d 2 π .( 2,4 ) 2
Ta có : Ω =
=
= 4,524 ( m 2 )
4
4
Thời gian tháo hết nước trong bể :
T=
2.π .H
m.ω. 2 gh
=
2.4,524.6
0,6.1,76.10 − 2 2.9,81.6
= 473,8 ( s ) = 7 ′53,8′′
2. Bể chứa nằm ngang :
Page 25 of 28
Cơ Học Lưu Chất
π
0
π
0
2
2
π .dh
Ω.dx
2 H .r. sin x.
4 H .r
sin xdx
T = 2∫
=2∫
=2 ∫
dx =
∫
−Q
−Q
mw 2 g .r π
cos x
r
0
0 − m.w 2 g .r. cos x
2
==
0
4 H .r
∫
mw 2 g .r
π
=
8H
mw 2 gh
d ( cos x )
2
cos x
8H
=
0
cos x π
mw 2 gh
8.6.1,2
=
2
= 1214 ( s ) = 18′44′′
0,6.1,76.10 − 2 2.9,81.1,2
BÀI TẬP CHƯƠNG VI
DÒNG CHẢY ỔN ĐỊNH, ĐỀU, CÓ ÁP TRONG ỐNG DÀI
Bài 6.1
Xác định lưu lượng chảy từ bể chứa A qua bể chứa B. Ống gang trong điều kiện bình thường.
Giải
Lưu lượng : Q = K
H
L
J =K
Ống gang bình thường : n = 0,0125
Modul lưu lượng :
8
K=
π .d 3
n.4
5
3
8
(
3,14.0,2 3
=
0,0125.4
5
= 0,314 m 3 / s
3
)
Lưu lượng :
Q=K
( )
H
20 − 15
= 0,314.
= 0,0241 m 3 = 24,1 ( l / s )
L
1000
Bài 6.2
Xác định cột nước H cần thiết để dẫn từ bể A qua bể B lưu lượng Q = 50L/s. Kích thước đường ống xem ở bài 1.
Giải
Từ bài 1 ta có : K = 0,314 m /s
3
Cột nước : H =
Q2
K2
L=
0,05 2
0,314 2
1000 = 21,5m
Bài 6.3
Page 26 of 28
Cơ Học Lưu Chất
Xác định đường kính d của một ống thép mới để dẫn lưu lượng Q = 200L/s dưới cột nước tác dụng H = 10m. chiều
dài ống L = 500m
Giải
Modul lưu lượng : Q = K
J ⇒K=
Q
=Q
J
(
L
500
= 0,2
= 1,414 m 3 / s
H
10
)
Ống sạch : n = 0,011
8
3
3
π .d 3
1,414 8 5 8
K 8 58
Đường kính : K =
⇒
d
=
n
4
=
0
,
011
4 = 0,325 ( m ) = 325mm
5
π
3
,
14
3
n.4
Bài 6.4
Một lưới phân phối có sơ đồ và các số liệu cho ở hình vẽ. Cột nước tự do ở cuối các đường ống h ≥ 5m. Ống gang
bình thường. Các số ở trong hình tam giác chỉ cao trình mặt đất tại các điểm. (Hình 6.4)
Yêu cầu :
1. Tính đường kính cho tất cả mạng chính và phụ.
2. Tính chiều cao tháp chứa.
3. Vẽ đường đo áp cho đường ống ABCDE.
Giải
Theo định nghĩa về đường ống chính ta chọn tuyến ống ABCDE và điểm E có cao trình không bé hơn so
với các điểm khác. Ngoải ra chiều dài của tuyếnlà dài nhất. Các đường ống còn lại được coi là ống nhánh.
1. Chọn đường kính và tính độ cao cho mạng ống chính.
Điểm
Đoạn
L
Q
d
γ
ống
(m)
(l/s)
(mm)
(m/s)
AB
500
65
300
0,92
θ2
K
hd
Độ cao
(l/s)
(m)
đo áp
1005,18
2,18
A
26,8
1,042
Page 27 of 28
Cơ Học Lưu Chất
B
24,62
BC
600
50
250
1,02
1,028
618,15
4,03
C
20,59
CD
300
15
150
0,85
1,0525
158,31
2,83
D
17,76
DE
500
5
100
0,64
1,098
53,69
4,76
E
13
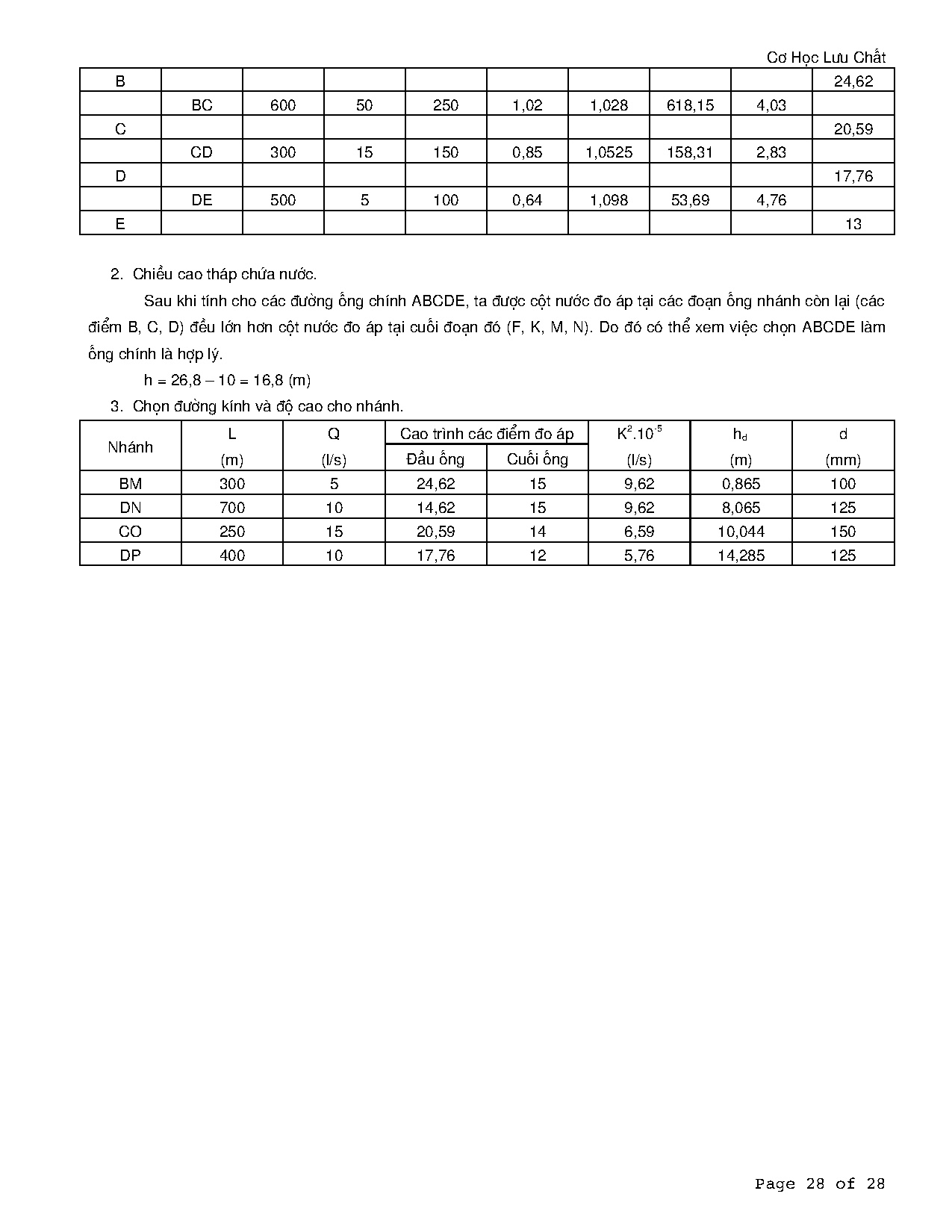
2. Chiều cao tháp chứa nước.
Sau khi tính cho các đường ống chính ABCDE, ta được cột nước đo áp tại các đoạn ống nhánh còn lại (các
điểm B, C, D) đều lớn hơn cột nước đo áp tại cuối đoạn đó (F, K, M, N). Do đó có thể xem việc chọn ABCDE làm
ống chính là hợp lý.
h = 26,8 – 10 = 16,8 (m)
3. Chọn đường kính và độ cao cho nhánh.
L
Q
Cao trình các điểm đo áp
K2.105
hd
d
(m)
(l/s)
Đầu ống
Cuối ống
(l/s)
(m)
(mm)
BM
300
5
24,62
15
9,62
0,865
100
DN
700
10
14,62
15
9,62
8,065
125
CO
250
15
20,59
14
6,59
10,044
150
DP
400
10
17,76
12
5,76
14,285
125
Nhánh
Page 28 of 28