Chapter 3, Part B
Time Series Analysis and Foreing
Trend Projection
Seasonality and Trend
Time Series Decomposition
1
Trend Projection
Nếu một chuỗi thời gian thể hiện xu hướng tuyến tính,
phương pháp bình phương tối thiểu có thể được dùng
để xác định đường xu hướng cho các dự báo trong
tương lai.
Bình phương tối thiểu, cũng được dùng trong phân tích
hồi quy, giúp xác định đường xu hướng dự báo duy
nhất giảm thiểu sai số bình phương trung bình giữa dự
báo đường xu hướng và các giá trị thực trong chuỗi
thời gian.
Biến độc lập là khoảng thời gian và biến phụ thuộc là
giá trị quan sát thực tế trong chuỗi thời gian.
2
Linear Trend Regression
Dùng phương pháp bình phương tối thiểu, công thức
cho dự báo xu hướng là:
Tt = b0 + b1t
trong đó:
Tt = linear trend fore in period t
b0 = intercept of the linear trend line
b1 = slope of the linear trend line
t = time period
3
Linear Trend Regression
Trong công thức dự báo xu hướng Tt = b0 + b1t
????1 =
????
????=1 ???? − ???? ???????? − ????
????
2
????
−
????
????=1
????0 = ???? − ????1 ????
Trong đó: Yt = value of the time series in period t
n = number of time periods (observations)
????= average values of the time series
???? = average value of t
4
Linear Trend Regression
Example: Auger’s Plumbing Service
The number of plumbing repair jobs performed by
Augers Plumbing Service in the last nine months is
listed on the right.
Month Jobs Month
Jobs
Fore the number of
409
March 353 August
repair jobs Augers will
April 387 September 399
perform in December
May
342 October
412
using the least squares
June 374 November 408
method.
July
396
5
Linear Trend Regression
(month) t ???? − ????
???? − ???? 2 Yt
???????? − ????
???? − ???? ???????? − ????
(Mar.) 1
(Apr.) 2
(May) 3
(June) 4
(July) 5
(Aug.) 6
(Sep.) 7
(Oct.) 8
(Nov.) 9
16
9
4
1
0
1
4
9
16
353
387
342
374
396
409
399
412
408
-33.67
0.33
-44.67
-12.67
9.33
22.33
12.33
25.33
21.33
134.68
-0.99
89.34
12.67
0
22.33
24.66
75.99
85.32
60
3480
Sum 45
-4
-3
-2
-1
0
1
2
3
4
444.00
6
Linear Trend Regression
???? = 45 9 = 5 and ????= 3480 9 = 386.667
????1 =
????
????=1 ???? − ???? ???????? − ????
????
2
????=1 ???? − ????
3480
=
= 7.12
60
????0 = ???? − ????1 ???? = 386.667 − 7.12 5 = 351.07
T10 = 351.07 + (7.12)(10) = 422.27
7
Using Excel’s Regression Tool
To Compute a Linear Trend Equation
Excel Worksheet (with data)
1
2
3
4
5
6
7
8
9
10
11
A
Month
March
April
May
June
July
August
September
October
November
B
Month
1
2
3
4
5
6
7
8
9
C
Jobs
353
387
342
374
396
409
399
412
408
8
Using Excel’s Regression Tool
To Compute a Linear Trend Equation
Step 1.
Step 2.
Step 3.
Step 4.
Click the Data tab on the Ribbon
In the Analysis group, click Data Analysis
Choose Regression from the list of Analysis Tools
When the Regression dialog box appears:
Enter C1:C10 in the Input Y Range box
Enter B1:B10 in the Input X Range box
Labels
Confidence Level
Enter 99 in the Confidence Level box
Output Range
Enter A13
Click OK
9
Using Excel’s Regression Tool
To Compute a Linear Trend Equation
Excel Regression Dialog Box
10
Using Excel’s Regression Tool
To Compute a Linear Trend Equation
Excel Regression Tool Output
A
B
C
D
E
F
G
H
I
7
8 SUMMARY OUTPUT
9
10
Regression Statistics
11 Multiple R
0.80076076
12 R Square
0.6412178
13 Adjusted R Square
0.5899632
14 Standard Error
16.2058191
15 Observations
9
16
17 ANOVA
18
df
SS
MS
F
Significance F
3285.6
3285.6 12.51044
19 Regression
1
0.00950792
1838.4 262.6286
20 Residual
7
21 Total
8
5124
22
Coefficients Standard Error
t Stat
23
P-value
Lower 95% Upper 95% Lower 95.0% Upper 95.0%
24 Intercept
349.66667
11.7732546 29.70009 1.26E-08 321.8273433
337.506 3084466359 390.8669745
25 Month
7.4 2.092162244 3.537011 0.009508 2.452822418
12.34718 0.07851317 14.72148683
26
11
Trend Projection
Example: Auger’s Plumbing Service
Fore for December (Month 10) using a
three-period (k = 3) weighted moving average with
weights of .6, .3, and .1
Month Jobs Month Jobs
for the newest to oldest
March 353 August 409
data, respectively. Then,
April 387 Septem. 399
compare this Month 10
May
342 October 412
weighted moving average
June 374 Novem. 408
fore with the Month 10
July
396
trend projection fore.
12
Trend Projection
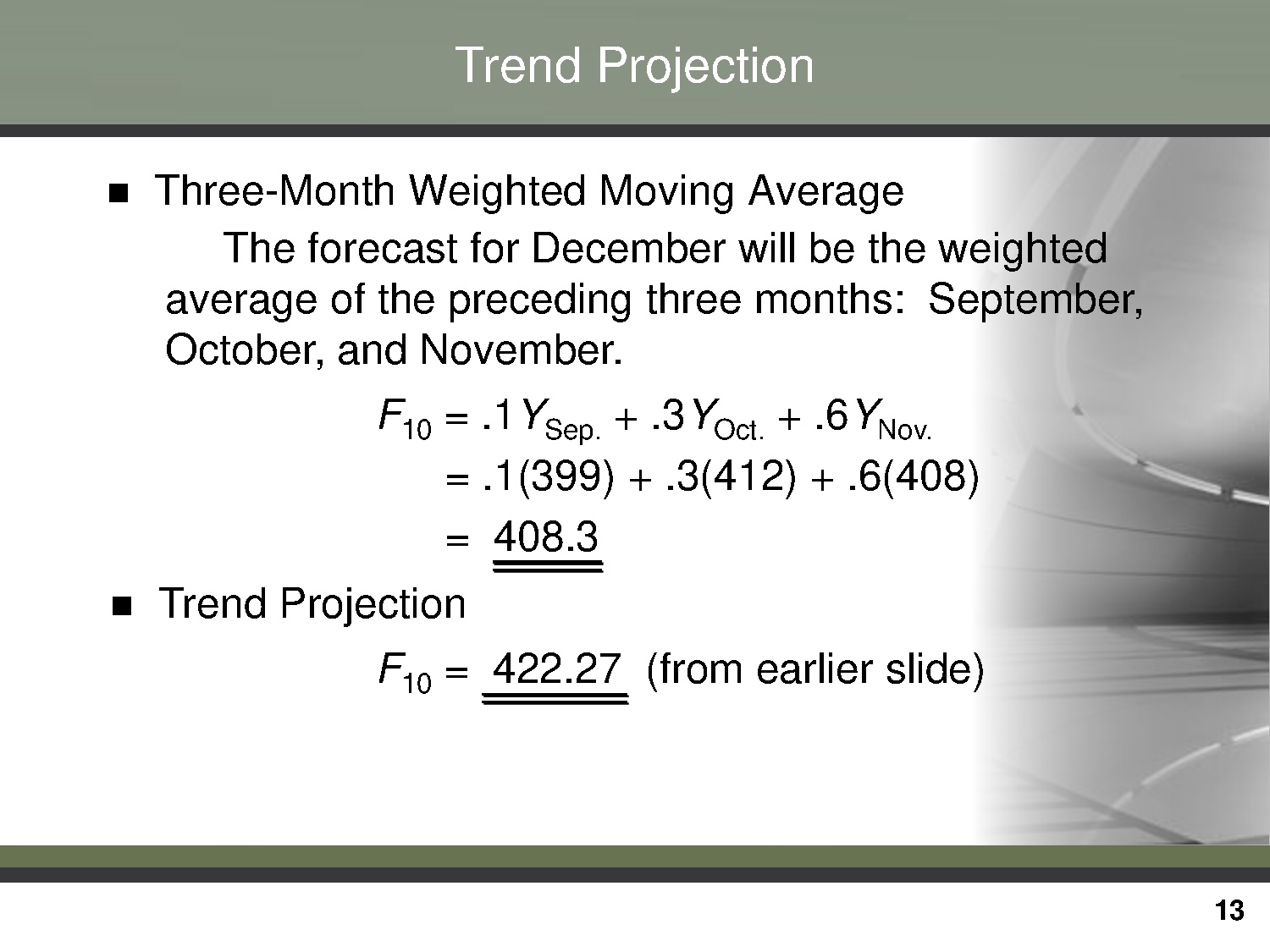
Three-Month Weighted Moving Average
The fore for December will be the weighted
average of the preceding three months: September,
October, and November.
F10 = .1YSep. + .3YOct. + .6YNov.
= .1(399) + .3(412) + .6(408)
= 408.3
Trend Projection
F10 = 422.27 (from earlier slide)
13
Nonlinear Trend Regression
Đôi khi chuỗi thời gian có xu hướng đường cong hay
phi tuyến.
Một loạt các hàm phi tuyến có thể được sử dụng để
ước lượng xu hướng của một chuỗi thời gian.
Một ví dụ là phương trình xu hướng bậc hai (quadratic):
Tt = b0 + b1t + b2t 2
Một ví dụ khác là phương trình xu hướng hàm mũ:
Tt = b0(b1)t
14
Nonlinear Trend Regression
Example: Cholesterol Drug Revenue
The annual revenue in millions of dollars for a
cholesterol drug for the first 10 years of sales is shown
below. A curvilinear
Year Revenue Year Revenue
function appears to
6
43.2
1
23.1
be needed to model
2
21.3
7
59.5
the long-term trend.
3
27.4
8
64.4
4
34.6
9
74.2
10
99.3
5
33.8
15
Using Excel’s Regression Tool
To Compute a Quadratic Trend Equation
Excel Worksheet (with data)
1
2
3
4
5
6
7
8
9
10
11
A
Year
1
2
3
4
5
6
7
8
9
10
B
Revenue
23.1
21.3
27.4
34.6
33.8
43.2
59.5
64.4
74.2
99.3
16
Excel’s Chart tools can be used to fit a polynomial
cur
...
...úng ta giả sử mối quan hệ được mô tả tốt nhất bằng
mô hình cộng hay mô hình nhân (additive or a
multiplicative model).
34
Time Series Decomposition
Additive Model
An additive model follows the form:
Yt = Trendt + Seasonalt + Irregulart
where:
Trendt = trend value at time period t
Seasonalt = seasonal value at time period t
Irregulart = irregular value at time period t
Một mô hình cộng phù hợp trong các tình huống
biến động theo mùa không phụ thuộc vào cấp độ
của chuỗi thời gian.
35
Time Series Decomposition
Multiplicative Model
A multiplicative model follows the form:
Yt = Trendt x Seasonalt x Irregulart
where:
Trendt = trend value at time period t
Seasonalt = seasonal value at time period t
Irregulart = irregular value at time period t
Một mô hình nhân là thích hợp, ví dụ, nếu biến
động theo mùa tăng lớn hơn khi doanh số bán hàng
tăng lên do xu hướng tuyến tính dài hạn.
36
Time Series Decomposition
Example: Terry’s Tie Shop
Year
1
2
3
4
Season
1
2
3
1856 2012 985
1995 2168 1072
2241 2306 1105
2280 2408 1120
Xác định dự báo cho doanh số bán hàng trung bình hàng tuần
trong năm thứ 5 cho mỗi mùa trong ba mùa.
37
Calculating the Seasonal Indexes
Bước 1. Tính trung bình trượt trung tâm (centered
moving averages - CMA).
Có ba mùa rõ rệt trong mỗi năm. Do đó, lấy
trung bình trượt ba mùa để loại bỏ các yếu tố
theo mùa và không thường xuyên. Ví dụ:
1st CMA = (1856 + 2012 + 985)/3 = 1617.67
2nd CMA = (2012 + 985 + 1995)/3 = 1664.00
Etc.
38
Calculating the Seasonal Indexes
Bước 2. Tập trung các CMA vào các khoảng thời gian
có giá trị nguyên.
CMA đầu tiên được tính trong bước 1 (1617,67) sẽ
được đưa vào mùa 2 của năm 1. Lưu ý rằng
trung bình trượt từ bước 1 đưa vào các khoảng
thời gian có giá trị nguyên vì n là một số lẻ.
39
Calculating the Seasonal Indexes
Dollar
Moving
Year Season Sales (Yt) Average
1
2
3
4
1
2
3
1
2
3
1
2
3
1
2
3
1856
2012
985
1995
2168
1072
2241
2306
1105
2280
2408
1120
(1856 + 2012 + 985)/3
1617.67
1664.00
1716.00
1745.00
1827.00
1873.00
1884.00
1897.00
1931.00
1936.00
40
Calculating the Seasonal Indexes
Các giá trị CMA có xu hướng làm trơn cả hai biến
động theo mùa và bất thường trong chuỗi thời gian.
CMA đại diện cho xu hướng trong dữ liệu và bất kỳ
biến đổi ngẫu nhiên nào không bị loại bỏ bằng cách
sử dụng trung bình trượt để làm trơn dữ liệu.
41
Calculating the Seasonal Indexes
Bước 3. Xác định các yếu tố theo mùa và bất thường (St It ).
Bằng cách chia giá trị thực tế cho trung bình trượt
của cùng khoảng thời gian, xác định hiệu ứng
kết hợp giữa yếu tố theo mùa và bất thường
trong chuỗi thời gian.
St It = Yt /(Moving Average for period t )
42
Calculating the Seasonal Indexes
Dollar
Moving
Year Season Sales (Yt) Average
1
2
3
4
1
2
3
1
2
3
1
2
3
1
2
3
1856
2012
985
1995
2168
1072
2241
2306
1105
2280
2408
1120
StIt
2012/1617.67
1617.67 1.244
1664.00 .592
1716.00 1.163
1745.00 1.242
1827.00 .587
1873.00 1.196
1884.00 1.224
1897.00 .582
1931.00 1.181
1936.00 1.244
43
Calculating the Seasonal Indexes
Bước 4. Xác định yếu tố theo mùa trung bình.
Trung bình của các giá trị St It tương ứng với mùa
đó:
Season 1: (1.163 + 1.196 + 1.181) /3
= 1.180
Season 2: (1.244 + 1.242 + 1.224 + 1.244) /4 = 1.238
Season 3: (.592 + .587 + .582) /3
= .587
3.005
44
Calculating the Seasonal Indexes
Bước 5. Scale the seasonal factors (St ).
Average the seasonal factors = (1.180 + 1.238 +
.587)/3 = 1.002. Then, divide each seasonal factor
by the average of the seasonal factors.
Season 1: 1.180/1.002 = 1.178
Season 2: 1.238/1.002 = 1.236
Season 3: .587/1.002 = .586
3.000
45
Calculating the Seasonal Indexes
Dollar
Moving
Year Season Sales (Yt) Avera