Chapter 2
Multiple Regression
Multiple Regression Model
Least Squares Method
Multiple Coefficient of Determination
Model Assumptions
Testing for Significance
Using the Estimated Regression Equation
for Estimation and Prediction
Categorical Independent Variables
Residual Analysis
Modeling Curvilinear Relationships
1
Multiple Regression Model
Mô hình hồi quy bội
Phương trình mô tả liên hệ giữa biến phụ thuộc
y và các biến độc lập x1, x2, . . . xp và một sai số là:
y = b0 + b1x1 + b2x2 + . . . + bpxp + e
Trong đó:
b0, b1, b2, . . . , bp là các tham số, và
e là biến ngẫu nhiên gọi là sai số
2
Multiple Regression Equation
Hàm hồi quy bội
Phương trình mô tả quan hệ giữa trung bình của
y với x1, x2, . . . xp là:
E(y) = b0 + b1x1 + b2x2 + . . . + bpxp
3
Estimated Multiple Regression Equation
Hàm hồi quy bội ước lượng
???? = b0 + b1x1 + b2x2 + . . . + bpxp
Một mẫu ngẫu nhiên đơn giản được dùng để tính
toán giá trị thống kê mẫu b0, b1, b2, . . . , bp là các giá
trị được được sử dụng như ước lượng điểm của các
tham số b0, b1, b2, . . . , bp.
4
Estimation Process
Multiple Regression Model
E(y) = b0 + b1x1 + b2x2 +. .+ bpxp + e
Multiple Regression Equation
E(y) = b0 + b1x1 + b2x2 +. . .+ bpxp
Unknown parameters are
Sample
x1 x2 . . . xp y
. .
. .
. .
. .
b 0, b 1, b 2, . . . , b p
b0, b1, b2, . . . , bp
provide estimates of
b 0, b 1, b 2, . . . , b p
Estimated Multiple
Regression Equation
???? = b0 + b1x1 + b2x2 + . . . + bpxp
Sample statistics are
b0, b1, b2, . . . , bp
5
Least Squares Method
Điều kiện bình phương tối thiểu
min
???????? − ???????? 2
Tính toán các hệ số
Công thức tính các hệ số hồi quy b0, b1, b2, . . . bp
liên quan đến ma trận đại số.
Dựa vào các phần mềm máy tính cho việc tính
toán này
6
Multiple Regression Model
Ví dụ: Khảo sát lương lập trình viên
Một công ty phần mềm thu thập dữ liệu mẫu gồm
20 lập trình viên. Phân tích hồi quy được sử dụng
để xem xét xem lương của lập trình viên có liên
quan đến số năm kinh nghiệm và điểm bài kiểm tra
năng lực của họ.
7
Multiple Regression Model
Exper. Test Salary
(Yrs.) Score ($000s)
4
7
1
5
8
10
0
1
6
6
78
100
86
82
86
84
75
80
83
91
24.0
43.0
23.7
34.3
35.8
38.0
22.2
23.1
30.0
33.0
Exper. Test
Salary
(Yrs.) Score ($000s)
9
2
10
5
6
8
4
6
3
3
88
73
75
81
74
87
79
94
70
89
38.0
26.6
36.2
31.6
29.0
34.0
30.1
33.9
28.2
30.0
8
Multiple Regression Model
Giả sử tin rằng lương (y) liên quan đến số năm
kinh nghiệm (x1) và điểm bài kiểm tra năng lực
(x2) qua mô hình sau:
y = b0 + b1x1 + b2x2 + e
Trong đó:
y = lương theo năm ($000)
x1 = số năm kinh nghiệm
x2 = điểm bài kiểm tra năng lực
9
Solving for the Estimates of b0, b1, b2
Least Squares
Output
Input Data
x1
x2
y
4 78 24
7 100 43
.
.
.
.
.
.
3 89 30
Computer
Package
for Solving
Multiple
Regression
Problems
b0 =
b1 =
b2 =
R2 =
etc.
10
Exper Test score Salary
1
4
78
24
2
7
100
43
…
…
…
…
19
3
70
28.2
20
3
89
30
11
12
Solving for the Estimates of b0, b1, b2
Regression Equation Output
p
Predictor
Coef
SE Coef
T
Constant
3.17394 6.15607 0.5156 0.61279
Experience 1.4039 0.19857 7.0702 1.9E-06
Test Score 0.25089 0.07735 3.2433 0.00478
13
Estimated Regression Equation
SALARY = 3.174 + 1.404(EXPER) + 0.251(SCORE)
14
Interpreting the Coefficients
Trong phân tích hồi quy bội, giải thích ý nghĩa các hệ
số hồi quy như sau:
bi cho thấy ước lượng thay đổi của y khi x tăng 1
đơn vị với tất cả các biến độc lập khác không đổi.
15
Interpreting the Coefficients
b1 = 1.404
Lương được kỳ vọng tăng $1,404 cho mỗi năm kinh
nghiệm tăng lên (khi điểm số bài kiểm tra năng lực
không đổi).
Hay: Khi số năm kinh nghiệm tăng lên 1 năm (điểm
số bài kiểm tra năng lực không đổi), lương được kỳ
vọng tăng $1,404
16
Interpreting the Coefficients
b2 = 0.251
Lương được kỳ vọng tăng $251 cho mỗi điểm
tăng thêm của bài kiểm tra năng lực của lập trình
viên (khi số năm kinh nghiệm không đổi).
17
Multiple Coefficient of Determination
Mối quan hệ giữa SST, SSR, SSE
SST
???????? − ???? 2 =
=
SSR + SSE
???????? − ???? 2 +
???????? − ???????? 2
Trong đó:
SST = total sum of squares
SSR = sum of squares due to regression
SSE = sum of squares due to error
18
Multiple Coefficient of Determination
ANOVA Output
Analysis of Variance
SOURCE
Regression
Residual Error
Total
DF
2
17
19
SS
500.3285
99.45697
599.7855
MS
250.164
5.850
F
42.76
P
0.000
SSR
SST
19
Multiple Coefficient of Determination
R2 = SSR/SST
R2 = 500.3285/599.7855 = .83418
20
Adjusted Multiple Coefficient
of Determination
Thêm vào các biến độc lập, mặc cho các biến thêm
vào không có ý nghĩa thống kê, làm cho sai số dự
báo nhỏ hơn, do đó làm giảm tổng sai số bình
phương, SSE.
Vì SSR = SST – SSE, khi SSE giảm, SSR tăng, dẫn
đến R2 = SSR/SST tăng lên.
Hệ số xác định mô hình hiệu chỉnh (adjusted multiple
coefficient of determination) có xét đến đánh đổi khi
cho thêm biến vào mô hình.
21
Adjusted Multiple Coefficient
of Determination
????????
????????
2
2
????−1
= 1 − (1 − ???? )
????−????−1
2
20 − 1
= 1 − 1 − .834179
= .814671
20 − 2 − 1
22
Assumptions About the Error Term e
Sai số e là biến ngẫu nhiên có trung bình bằng 0.
Phương sai của e , ký hiệu là 2, giống nhau ở tất cả
giá trị của các biến độc lập.
Giá trị của các e là độc lập.
Sai số e là biến ngẫu nhiên có phân phối chuẩn, phản
ánh độ lệch giữa giá trị y quan sát với giá trị y mong đợi
từ b0 + b1x1 + b2x2 + . . + bpxp.
23
Testing for Significance
Trong hồi quy tuyến tính đơn, kiểm định t và F cho
cùng kết luận.
Trong hồi quy bội, kiể
...
...06
-1.059048
0.994921
-0.246689
42
Standardized Residual Plot Against ????
43
Categorical Independent Variables
Trong nhiều trường hợp có thể gặp các biến độc lập có
tính chất phân loại, ví dụ giới tính (nam, nữ),
hình thức thanh toán (tiền mặc, check, thẻ tín dụng) …
Ví dụ, x3 đại diện cho biến giới tính, trong đó x3 = 0
tương ứng với giới tính nam và x3 = 1 tương ứng với
giới tính nữ
Lúc này, x3 được gọi là biến giả.
44
Categorical Independent Variables
Ví dụ: Khảo sát lương lập trình viên
Mở rộng hơn cho khảo sát về lương lập trình viên,
giả sử rằng ban quan lý cũng tin rằng lương hàng
năm của lập trình viên liên quan đến việc họ có
bằng tốt nghiệp về khoa học máy tính hay hệ thống
thông tin.
45
Categorical Independent Variables
Exper. Test
Salary
(Yrs.) Score Degr. ($000)
4
7
1
5
8
10
0
1
6
6
78
100
86
82
86
84
75
80
83
91
No
Yes
No
Yes
Yes
Yes
No
No
No
Yes
24.0
43.0
23.7
34.3
35.8
38.0
22.2
23.1
30.0
33.0
Exper. Test
Salary
(Yrs.) Score Degr. ($000)
9
2
10
5
6
8
4
6
3
3
88
73
75
81
74
87
79
94
70
89
Yes
No
Yes
No
No
Yes
No
Yes
No
No
38.0
26.6
36.2
31.6
29.0
34.0
30.1
33.9
28.2
30.0
46
Categorical Independent Variables
Hàm hồi quy
???? = b0 + b1x1 + b2x2 + b3x3
Trong đó:
???? = lương hàng năm ($1000)
x1 = số năm kinh nghiệm
x2 = điểm bài kiểm tra năng lực
x3 = 0 nếu không có bằng cấp liên quan
1 nếu có bằng cấp liên quan
x3 là một biến giả
47
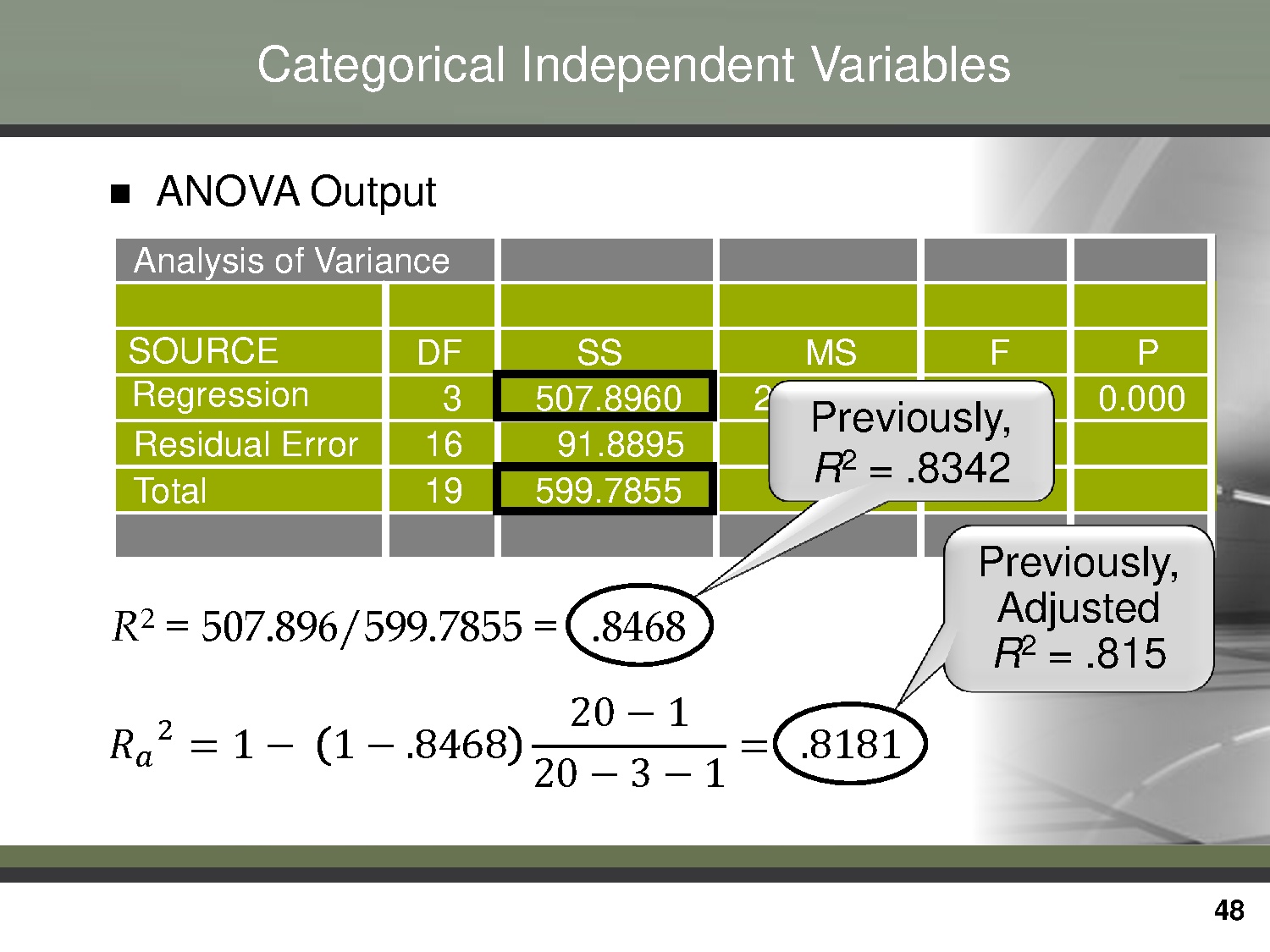
Categorical Independent Variables
ANOVA Output
Analysis of Variance
SOURCE
Regression
Residual Error
Total
DF
3
16
19
SS
507.8960
91.8895
599.7855
MS
F
269.299
29.48
Previously,
5.743
2
R = .8342
R2 = 507.896/599.7855 = .8468
????????
2
P
0.000
Previously,
Adjusted
R2 = .815
20 − 1
= 1 − 1 − .8468
= .8181
20 − 3 − 1
48
Categorical Independent Variables
Regression Equation Output
Predictor
Constant
Experience
Test Score
Grad. Degr.
Coef
7.945
1.148
0.197
2.280
SE Coef
7.382
0.298
0.090
1.987
T
1.076
3.856
2.191
1.148
p
0.298
0.001
0.044
0.268
Not significant
49
More Complex Categorical Variables
Nếu một biến phân loại có k biểu hiện, sẽ cần k - 1
biến giả, với mỗi biến giả có giá trị 0 hoặc 1.
Ví dụ, một biến với 3 biểu hiện A, B, và C có thể được
đại diện bởi biến giả x1 và x2 với giá trị tương ứng
(0, 0) cho A, (1, 0) cho B, và (0, 1) cho C.
Cần thận trọng khi xác định và giải thích biến giả.
50
More Complex Categorical Variables
Ví dụ, một biến phân loại về giáo dục được đại
diện bởi các biến giả x1 và x2 với giá trị như sau:
Bằng cấp cao nhất x1
x2
Cử nhân
Thạc sĩ
Tiến sĩ
0
0
1
0
1
0
51
Modeling Curvilinear Relationships
Example: Sales of Laboratory Scales
A manufacturer of laboratory scales wants to
investigate the relationship between the length of
employment of their salespeople and the number of
scales sold.
The table on the next slide gives the number of
months each salesperson has been employed by the
firm (x) and the number of scales sold (y) by 15
randomly ed salespersons.
52
Modeling Curvilinear Relationships
Example: Sales of Laboratory Scales
Months Sales
41
106
76
104
22
12
85
111
275
296
317
376
162
150
367
308
Months Sales
40
51
9
12
6
56
19
189
235
83
112
67
325
189
53
Modeling Curvilinear Relationships
Excel’s Chart tools can be used to develop a scatter
dia