Digital Signal Processing
John G. Proakis Dimitris K. Manolakis
Fourth Edition

Pearson Education Limited
Edinburgh Gate
Harlow
Essex CM20 2JE
England and Associated Companies throughout the world
Visit us on the World Wide Web at: www.pearsoned.co.uk
© Pearson Education Limited 2014
All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted
in any form or by any means, electronic, mechanical, photocopying, recording or otherwise, without either the
prior written permission of the publisher or a licence permitting restricted copying in the United Kingdom
issued by the Copyright Licensing Agency Ltd, Saffron House, 6–10 Kirby Street, London EC1N 8TS.
All trademarks used herein are the property of their respective owners. The use of any trademark
in this text does not vest in the author or publisher any trademark ownership rights in such
trademarks, nor does the use of such trademarks imply any affiliation with or endorsement of this
book by such owners.

ISBN 10: 1-292-02573-5
ISBN 13: 978-1-292-02573-5

British Library Cataloguing-in-Publication Data
A catalogue record for this book is available from the British Library
Printed in the United States of America

P

E

A

R

S

O

N

C U

S T O

M

L

I

B

R

A

R Y

Table of Contents

1. Introduction
John G. Proakis/Dimitris G. Manolakis

1

2. Discrete-Time Signals and Systems
John G. Proakis/Dimitris G. Manolakis

43

3. The z-Transform and Its Application to the Analysis of LTI Systems
John G. Proakis/Dimitris G. Manolakis

151

4. Frequency Analysis of Signals
John G. Proakis/Dimitris G. Manolakis

229

5. Frequency-Domain Analysis of LTI Systems
John G. Proakis/Dimitris G. Manolakis

307

6. Sampling and Reconstruction of Signals
John G. Proakis/Dimitris G. Manolakis

395

7. The Discrete Fourier Transform: Its Properties and Applications
John G. Proakis/Dimitris G. Manolakis

461

8. Efficient Computation of the DFT: Fast Fourier Transform Algorithms
John G. Proakis/Dimitris G. Manolakis

523

9. Implementation of Discrete-Time Systems
John G. Proakis/Dimitris G. Manolakis

577

10. Design of Digital Filters
John G. Proakis/Dimitris G. Manolakis

669

11. Multirate Digital Signal Processing
John G. Proakis/Dimitris G. Manolakis

767

12. Linear Prediction and Optimum Linear Filters
John G. Proakis/Dimitris G. Manolakis

841

13. Adaptive Filters
John G. Proakis/Dimitris G. Manolakis

899

I

14. Appendix: Random Number Generators
John G. Proakis/Dimitris G. Manolakis

981

15. Appendix: Tables of Transition Coefficients for the Design of Lnear-Phase FIR Filters
John G. Proakis/Dimitris G. Manolakis

987

16. References and Bibliography

II

John G. Proakis/Dimitris G. Manolakis

993

Index

1007

Introduction

Digital signal processing is an area of science and engineering that has developed
rapidly over the past 40 years. This rapid development is a result of the significant
advances in digital computer technology and integrated-circuit fabrication. The digital computers and associated digital hardware of four decades ago were relatively
large and expensive and, as a consequence, their use was limited to general-purpose
non-real-time (off-line) scientific computations and business applications. The rapid
developments in integrated-circuit technology, starting with medium-scale integration (MSI) and progressing to large-scale integration (LSI), and now, very-large-scale
integration (VLSI) of electronic circuits has spurred the development of powerful,
smaller, faster, and cheaper digital computers and special-purpose digital hardware.
These inexpensive and relatively fast digital circuits have made it possible to construct
highly sophisticated digital systems capable of performing complex digital signal processing functions and tasks, which are usually too difficult and/or too expensive to
be performed by analog circuitry or analog signal processing systems. Hence many
of the signal processing tasks that were conventionally performed by analog means
are realized today by less expensive and often more reliable digital hardware.
We do not wish to imply that digital signal processing is the proper solution for
all signal processing problems. Indeed, for many signals with extremely wide bandwidths, real-time processing is a requirement. For such signals, analog or, perhaps,
optical signal processing is the only possible solution. However, where digital circuits are available and have sufficient speed to perform the signal processing, they
are usually preferable.
Not only do digital circuits yield cheaper and more reliable systems for signal
processing, they have other advantages as well. In particular, digital processing
hardware allows programmable operations. Through software, one can more eas-

From Chapter 1 of Digital Signal Processing: Principles, Algorithms, and Applications, Fourth Edition.
John G. Proakis, Dimitris G. Manolakis. Copyright © 2007 by Pearson Education, Inc. All rights reserved.

1
...
--------------------------------------
...lateral z-transform, 160, 210
Unipolar, 416
Unit circle, 178-181, 199, 201-202, 204-206, 213, 218,
222, 224, 227, 266-269, 322-323, 325-330,
337, 340, 343, 345, 347, 349, 351, 363-365,
367, 381, 475, 554-557, 569, 584, 596, 612,
629, 631-634, 641, 648-649, 651-652, 659,
673, 678, 692-694, 718, 720-722, 725, 728,
730, 748, 852-854, 862, 873-874, 891,
895-896, 931, 996, 1004, 1006
Unit step sequence, 49, 80, 103, 105, 217, 268, 674,
930
Units, 52, 54, 63-65, 69, 79, 81, 120-121, 145, 336,
391, 478-479, 485-486, 684, 718, 772, 868,
871
of time, 52, 63, 69, 486, 718
Unity, 45, 47, 73, 90, 110, 209, 238, 315, 335, 338,
345, 471, 568, 599, 612, 675, 698, 754, 793,
931, 935, 941, 982
unknown, 2, 29, 56, 126-127, 331, 334, 357-358,
366-368, 761-763, 900-903, 906, 916
Us, 2, 8, 15-16, 23, 26-27, 31-32, 43, 61, 63, 77, 79,
81, 85, 88, 91, 97-99, 101, 105, 109-111,
118-119, 121-122, 127, 154, 161, 164, 181,
198, 205, 215, 218, 240-241, 256, 258-259,
261, 275, 279, 308-309, 318, 321, 325-326,
331-332, 335, 350, 358, 362, 368-369,
399-400, 480, 496, 502-503, 525, 531, 539,
548, 552-554, 557-559, 561-562, 564,
599-600, 603, 608, 610-612, 616, 619-623,
630, 638, 642-643, 645-646, 648-649, 698,
713, 724-725, 728, 741, 761, 773, 794-799,
802-803, 811-812, 814-815, 835, 843-844,
848-850, 861-862, 866-869, 878-879,
911-913, 920, 923, 939, 948, 950-951
Utility, 37

V
Value, 6, 8-11, 13, 15, 17, 19-20, 27, 31-33, 36, 38,
44-45, 50, 57-58, 63, 73-74, 76, 88-89,
92-94, 100, 105-106, 123, 127, 147, 164,
172-173, 185, 207, 213, 220-222, 227,
233-234, 238-239, 259, 269, 299, 315-316,
326, 331-333, 340-341, 345, 379, 383-384,
417, 441, 445, 456, 470, 484, 524, 552-553,
555-556, 562, 564, 568, 572-573, 580,
592-593, 622-626, 636, 638-639, 643, 651,
664, 693, 700-701, 731-733, 736, 757, 762,
770-771, 773, 785, 843-844, 849-851,
855-857, 863-864, 872, 889, 912-914,
934-935, 949-950, 977, 981-983
added, 552, 934
Values, 4, 9-11, 16, 18-20, 22-24, 28, 32-33, 36, 38,
40, 44, 48, 50, 55, 57-58, 63, 68-69, 73,
76-77, 79-80, 84-86, 88-90, 92-96, 110, 116,
121, 123, 127, 131, 140, 142-143, 152-154,
174, 182-185, 187, 206, 210, 238-239, 246,
339, 345-346, 351, 361, 368-369, 383, 406,
413, 433, 442, 445-446, 452, 459, 465-466,
475, 486, 495, 511-513, 516-517, 524-525,
527, 529, 552-554, 556, 566-567, 569, 571,
579-580, 598, 630, 637, 639, 642, 664,
687-688, 690-691, 693, 725, 741, 744, 754,
758, 762, 769-771, 812, 857, 890, 906-907,

1013

931-932, 967, 973, 976-977, 987
Variables, 2-3, 6, 8, 21-25, 160, 165, 184, 275,
397-398, 439, 550, 562, 718, 721, 730-731,
778, 843-845, 925, 944, 983, 985-986, 996
Variance, 419, 445-446, 449, 456, 562-563, 565-567,
572, 574-575, 637, 646-648, 650, 652, 663,
665-666, 761, 763, 844, 848-849, 851, 864,
874, 880, 883, 892, 894, 897, 933, 947,
971-972, 978-979, 984-986
Variations, 262, 415, 438, 452, 507, 892, 905, 907,
927-929, 935, 946, 966, 974
vector, 7-8, 299, 326, 357, 472, 511-512, 547, 549,
806, 830, 866-867, 882, 884, 894-895,
924-932, 934, 936-941, 943-944, 948-950,
955, 957, 962-963, 965-967, 975-976
Velocity, 274
Vertical, 34, 426, 441
Vertical line, 426, 441
Vibrations, 232
Vocal tract, 3, 612, 917
VOL, 391, 993-1006
Voltage, 39, 237, 397, 415, 421
Volume, 908

W
Walls, 146
Warping, 730
Wave, 8, 253, 260, 265, 298, 512, 560, 654
Waveforms, 231-232, 842-843, 999
Web, 962, 964-969
Weight, 37, 707, 997
Weighted moving average, 114
Weighting function, 334, 698-700, 706, 708, 714
Well, 1, 5, 11, 17, 48, 55, 61, 97, 181, 185, 214, 231,
269-270, 342, 357, 375, 434, 524, 566-567,
676, 717, 733, 738, 754, 763, 795, 860,
867-868, 878, 885, 907, 913
White, 8, 127, 231-232, 332, 334, 419, 426, 449, 513,
561-562, 646-648, 665, 668, 761, 852-855,
864, 874-876, 880, 883, 886, 893-894,
896-897, 918, 933, 976-979, 997, 1005
White noise, 127, 334, 419, 449, 513, 561, 646-648,
665, 668, 761, 852-855, 864, 874-876, 880,
883, 893-894, 896-897, 918, 976, 978-979,
997
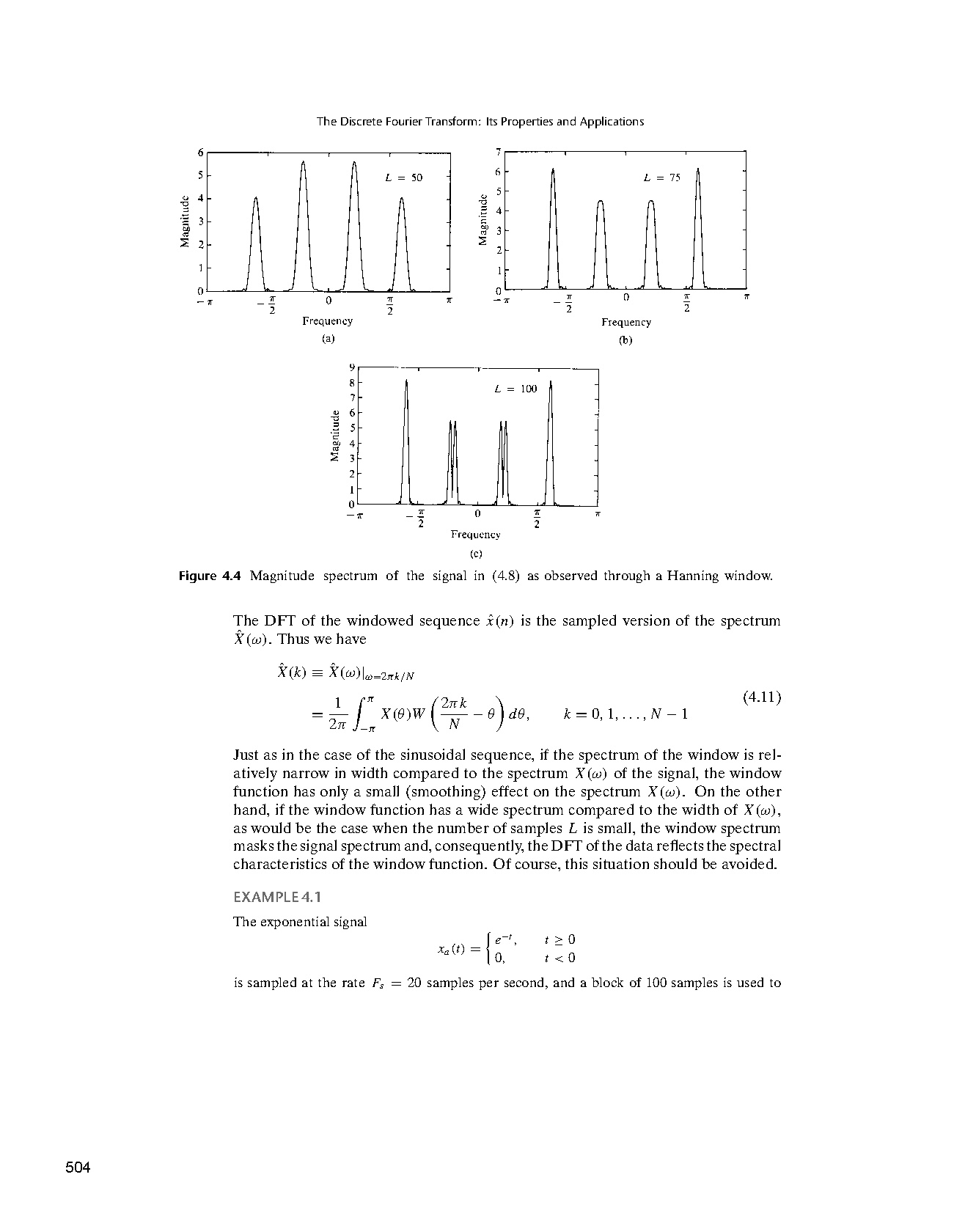
Window function, 504, 506-507, 680-681, 685
Windowing, 294, 370, 501-502, 505
theorem, 294
Wire, 907-908
Wood, 371, 1006
Word, 6, 35-36, 416, 421, 577-579, 615, 621, 627,
637, 642, 654, 664, 946, 970, 1001
Work, 88, 232, 262, 361, 452, 655, 751, 831, 892, 947,
1003

X
X rays, 275

Y
Yield, 1, 24-25, 60, 63, 70, 76, 81-82, 120, 166, 213,
216, 321, 401, 429, 470, 474, 486, 496-497,
559, 680, 691, 751, 756, 793, 812, 821, 890
Yielding, 741

Z
Zero frequency, 271, 573, 708
Zero placement, 337, 341, 370
z-transform, 60, 151-228, 265-269, 321, 323, 326,
330, 359, 366, 369-370, 380, 383, 449, 554,
556, 559-560, 569-570, 572, 578, 583,
591-592, 729, 775, 778, 785, 817-818, 825,
886-888, 893-894, 1003
bilateral, 159
convolution property, 169, 181, 213, 218-219
differentiation property, 168
linearity property, 161, 188
region of convergence (ROC), 152
time-shifting property, 163, 168, 182
two-sided, 158-160, 171, 195, 209-211, 213, 219,
887
unit circle, 178-181, 199, 201-202, 204-206, 213,
218, 222, 224, 227, 266-269, 323, 326,
330, 475, 554, 556, 569, 852, 893

1014